Vieta root flipping or Vieta jumping is a proof technique by generating another solution to a given equation. The process is based off of Vieta's formulas, which link the different roots of a polynomial. For example, in a quadratic,
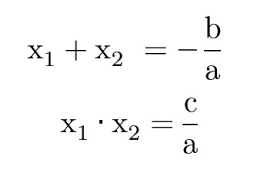
Where x1 and x2 are the two roots of the quadratic equation,
But why is this useful? It turns out that this equation has a very nifty application in number theory. The idea is simple, you take some quadratic equation, and you have one solution. To find the other solution, simply use Vieta's formula! But why exactly is this such a powerful technique?
Consider this problem, from the 2007 British Mathematical Olympiad Round 2 question 2:
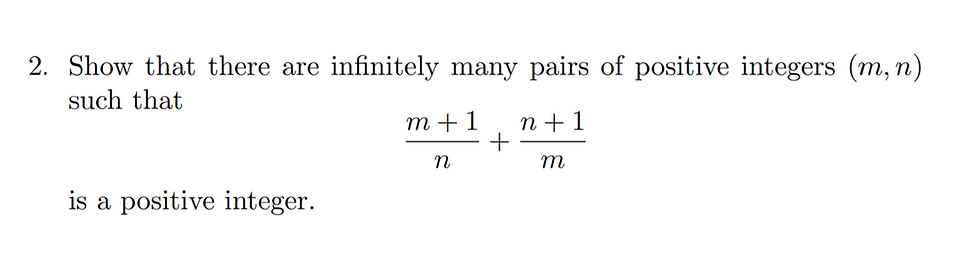
We're not going to cover the whole problem, but I'll leave it to the reader to see if you can use the problem in the question to end up with,
Where k is some positive integer.
Now we can use a neat trick, and look at the following quadratic equation,
Now, we can notice that x = m is a root of this quadratic equation. Now the Vieta's formula comes into play. We have one root of the equation, and so the other one is,
But what did we actually do here? After applying Vieta's second formula shown above, we managed to generate another solution to original equation!
The key with this problem is to realise that we don't have to stop here. Instead we can apply Vieta's formula again, to generate another solution, and again and again, as many times as we like.
This process can be repeated an infinite number of times, and so we can generate an infinite number of distinct positive integer solutions. And we are done!
Now if you're feeling brave, here is another problem you might like to try using a very similar technique,
(Both questions here were taken directly from https://bmos.ukmt.org.uk/home/bmo.shtml. Be sure to check it out, and the rest of the amazing UKMT resources as well!)
Stay tuned for next time when we will look at Fermat's Method of infinite descent!
If you have any questions about Vieta jumping, please feel free to contact me, and I will reply as soon as possible! Meanwhile, maybe this will help: https://en.wikipedia.org/wiki/Vieta_jumping
Comments